Editor’s note: We’re revisiting this series on navigating by the sun, moon, stars and planets in the age of GPS because celestial nav is not only a viable backup to satellite navigation, but it’s also a skill that ocean voyagers should have in their toolkit. During the next few issues, we’ll cover all the basic knowledge you’ll need to get up to speed on this elegant and rewarding technique for finding your way at sea. Click for Part 1 and Part 2.
 |
|
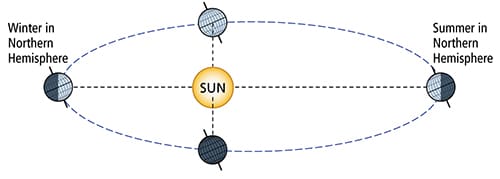
To the left, the North Pole is pointed away from the sun (our winter) and the sun’s declination is south. As the Earth continues its course around the sun, the sun heads north until the spring equinox where the sun is on the equator. By the summer solstice, the North Pole is pointing toward the sun and the declination of the sun reaches its most northerly point. At the autumnal equinox, the sun’s declination returns to 0°. (The elliptical orbit of the Earth is greatly exaggerated here.) |
In this installment, we’ll discuss the navigational astronomy of the sun, the celestial sphere, the coordinate system used on the celestial sphere and also the navigational triangle.
Navigational astronomy
You probably haven’t thought about it much, but the motion of the sun across the sky isn’t the true motion of the sun; it’s properly called the sun’s apparent motion. To people on the surface of the Earth, the sun appears to move from east to west. We see the sun rise in the east each morning and set in the west each evening. Actually, the Earth is rotating on its axis from west to east, which causes this apparent rising and setting of the sun. In terms of celestial navigation, we are primarily concerned with this apparent sun. There is a simple reason for this: The sun in the sky is the only sun we have available for making sextant observations.
 |
|
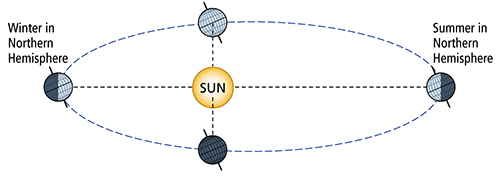
This part of the Nautical Almanac is found at the bottom of the right-hand daily page. The equation of time is shown for both noon and midnight on each of the three days. The meridian passage is determined by rounding off the equation of time at 1200 each day. |
The sun has a starting point each day: the Greenwich meridian, 0° longitude. Its progress is then measured westward from this point for the full 360° around the Earth until it reaches the Greenwich meridian again the next day. The time that the sun passes the Greenwich meridian each day is listed in the daily pages of the Nautical Almanac. This event is called “meridian passage” and occurs at every meridian of longitude each day when the sun is on that meridian. The sun rarely crosses at exactly 1200 (more on that below).
The Nautical Almanac chronicles the sun’s daily progress with two columns of information describing the sun’s position: GHA and declination.
GHA stands for Greenwich Hour Angle and is a measure of the distance that the apparent sun has traveled west from its starting point on the Greenwich meridian. GHA cycles through 360° every day. This is logical because we know that the sun goes around the Earth once per day. By contrast to GHA’s daily change through 360°, the declination value changes at a snail’s pace.
 |
|
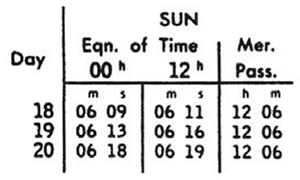
Although in reality the Earth is rotating from west to east, the apparent motion of the sun is from east to west. This westward progress each day is measured by GHA. |
While declination does change each hour, the change is usually measured in tenths of minutes and not in degrees. Declination measures the sun’s distance north or south of the equator. This declination is a result of the Earth’s tilt on its axis relative to the path that it takes around the sun.
The plane formed by the Earth’s orbit around the sun is called the Plane of the Ecliptic (makes sense because eclipses take place on this plane). The Earth’s axis tilts at 23.5° to this plane and that tilt is what accounts for our seasons on Earth.
The sun’s declination completes its cycle once a year. At the summer solstice — June 21 in the Northern Hemisphere — the sun’s declination reaches its furthest point north, 23.5° N. It then heads south until Sept. 22, the autumnal equinox, when the sun’s declination is 0°. The two equinoxes are the only days of the year when the day and the night are of equal length. These are also the only times when the sun rises directly in the east and sets directly in the west. The winter solstice in the Northern Hemisphere is Dec. 22 when the sun reaches 23.5° S. The vernal, or spring, equinox is on March 21. Many globes have lines circling them at 23.5° N and 23.5° S. These lines are labeled the Tropic of Cancer and the Tropic of Capricorn, respectively. It is only when an observer is between these lines that they will see the sun directly overhead.
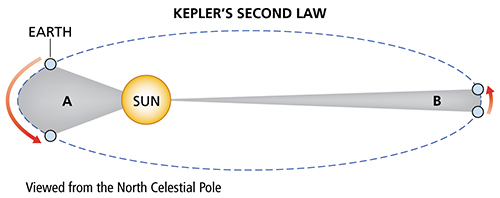 |
|
This shows the orbit of the Earth around the sun. Kepler’s Second Law indicates that a straight line joining the sun and a planet sweeps over equal areas in equal intervals of time. Thus, the closer the Earth is to the sun in its orbit, the farther it must travel each day to create an equal area. In the illustration, if area A is the same as area B, it is clear that the distance traveled by the Earth to create A is much greater. At the two extremes (the fastest and slowest movement of the Earth) the effect on the equation of time will be the greatest. Both the elliptical nature of the Earth’s orbit and the distance traveled in the course of a day have been greatly exaggerated here. |
The reason that meridian passage is not 1200 at the Greenwich meridian each day, and the reason that GHA changes from day to day, is that the sun does not travel around the Earth in exactly 24 hours. The apparent sun is inconsistent. Because astronomers, and others of us, don’t like to constantly have to adjust for inconsistencies caused by the fluctuations of the apparent sun, scientists invented something called the mean sun (mean as in average, not nasty). The mean sun is the one that all clocks are set to. It goes around the Earth exactly once every 24 hours. But, of course, we can’t see the mean sun, only the apparent sun.
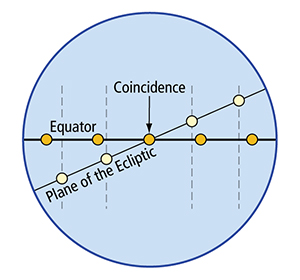 |
|
The path of the sun across the surface of the Earth goes from the winter solstice through the equinox to the summer solstice. But mean time is measured as if the path of the sun were along the equator. |
The difference between the mean sun and the apparent sun is called the equation of time. This sounds rather imposing and complicated (and it must be fairly difficult to figure it out), but it has been reduced to a simple answer on each daily page of the Nautical Almanac. Later in this series we’ll learn more about how to use this number.
The three factors influencing the time difference between the mean and apparent sun are: 1) the elliptical nature of the Earth’s rotation around the sun, 2) the measurement of the sun’s path along the equator instead of along the ecliptic, and 3) the change in the Earth’s rotational speed. The first two are shown in accompanying illustrations. The last factor, the change in the speed of the Earth’s rotation, is insignificant for the purposes of marine navigation, so we need not worry about it as a practical matter.
The celestial sphere: GHA and declination
In the previous paragraphs, we looked at the actual physical forces that govern the motion of the sun through the sky. In that discussion, however, we used the Copernican model of the sun at the center of the solar system. As navigators, though, we use a different approach to the positions and motions of celestial bodies. We favor the system used by Greek philosopher and scientist Aristotle. That is, the Earth is at the center of things and is surrounded by a giant sphere on which all the celestial bodies move. We call this concept the celestial sphere. Though the concept of an Earth-centered solar system was rejected by astronomers long ago, it’s still a useful tool for celestial navigators. It’s a way of simplifying celestial mechanics in a way that serves our needs.
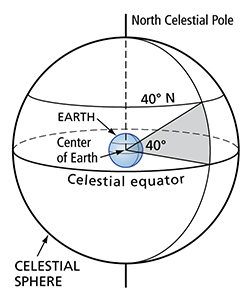 |
|
Declination is measured just the way latitude is. The declination is just a measure of the angle at the center of the Earth formed by the plane of the equator and going out to the celestial body. In fact, the same line from the center of the Earth will go through the parallel for 40° latitude and 40° declination as shown here. |
The coordinates used to describe the position of celestial bodies on this celestial sphere are similar to the coordinates we use to describe locations on Earth. On the globe we use latitude and longitude, and we use a similar system up on the celestial sphere. To get a sense of how this works, imagine the Earth as a translucent shell inscribed with lines of latitude and longitude and with a light bulb at its center. When the light is on, it projects all of the coordinate lines from Earth up onto the celestial sphere. Thus, directly over the equator on Earth is the celestial equator. And, right over the North Pole is the North Celestial Pole.
On Earth, we measure latitude north and south from 0° at the equator to 90° at the poles. On the celestial sphere, north and south are measured the same way, but instead of latitude the parallels are called “declination.” So, starting at 0° at the celestial equator, declination measures 90° north and south to the poles. Declination should therefore always be labeled “north” or “south” just like latitude.
Measuring east and west on the celestial sphere is a little bit different from the system of longitude on Earth. On the globe, all meridians of longitude intersect at the poles and are spaced farthest apart at the equator. This same system holds true on the celestial sphere. The only difference is the way longitude is measured.
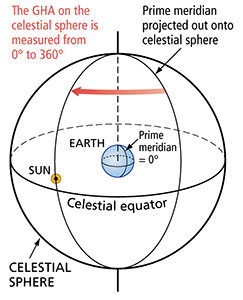 |
|
GHA is measured west only. Starting at 0° on the projection of the Greenwich meridian, the GHA increases through 360°. In this diagram, the GHA of the sun would be about 80° measured west from the prime meridian on the celestial sphere to the meridian that the sun is on. |
On Earth, the meridians are labeled starting at 0° at Greenwich and moving around the globe both east and west to 180° at the International Date Line. On the celestial sphere, the projection of the Greenwich meridian is still used as the 0° starting point. From there, what we call Greenwich Hour Angle (GHA) on the celestial sphere is measured westwardly around to 360°. For this reason, GHA is not labeled; it only measures west from the Greenwich meridian.
So in order to describe the position of a body on the celestial sphere, two numbers are required: declination and GHA. These are found in the Nautical Almanac for every second of the year.
The navigational triangle
All of celestial navigation is based on something called the navigational triangle. This triangle illustrates all of the terms and concepts encountered during the sight reduction process. Luckily, we don’t need to use spherical trigonometry to calculate the angles and sides of the triangle itself. We will use the sight reduction tables that will perform the calculations for us. It is important, however, to know how the navigational triangle works so we can use that knowledge as a way to check and see if we are doing things correctly. So we’ll discuss just enough of the triangle here to give you the ability to self-check your work.
 |
|
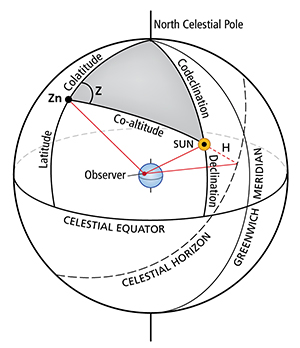
The navigational triangle is the area shaded in gray. Here, the sun is east of the observer and Z=Zn. |
In the accompanying figure (left), we see a case of a morning sun sight. Note that the sun is to the east of the observer’s zenith. Zenith is the point on the celestial sphere directly overhead.
Because the arc distance (measured in degrees instead of miles) from the equator to the observer (latitude) can be projected to the celestial sphere, it is the same distance and therefore labeled “latitude.” The distance from the zenith to the north celestial pole is 90° minus the latitude, and we call this the colatitude (because it is the compliment of latitude — two numbers added together that result in 90 are called complimentary numbers). In other words, if we add latitude to colatitude we get 90°.
The sun’s declination is the distance from the equator to the sun. Just like in the previous case of the observer’s zenith, the distance from the sun to the pole is 90° minus the declination, or codeclination.
The angle from the horizon to the zenith is 90°; the horizon is horizontal and the zenith is directly overhead. The angle measured with the sextant is “H” and that extends from the horizon to the sun. This means that the co-altitude (90° minus H) extends from the sun to the zenith.
 |
|
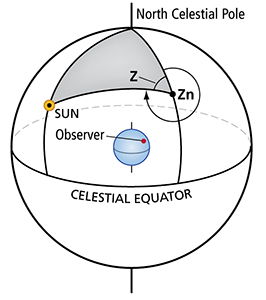
With the sun to the west of the observer’s zenith, the Z measures an angle from north westward. Zn, however, must start eastward from north and so Zn = 360 – Z when the body is west of the observer. |
So how do we calculate this triangle? A spherical triangle can be solved if any two sides and the enclosed angle are known. We know the colatitude and the codeclination, so all we need is the angle up at the North Celestial Pole. This interior angle is called the meridian angle and abbreviated “t.” To use the sight reduction table HO 249 we cannot use t, however. Instead, the tables require a different measure of that angle called Local Hour Angle (LHA). GHA measures west from Greenwich to the sun; LHA measures west from our longitude (local to us) to the sun. In this case, LHA measures almost around the Earth.
Once we go to the tables, we get two pieces of information: Z and Hc. Hc is the calculated altitude of the sun — the table subtracts it from 90° after figuring out the co-altitude. The other figure we get from the tables, Z, is the azimuth angle. This is the angle inside the triangle at the zenith.
This is great, but we really want the true bearing to the sun. By convention, bearings are measured starting with 0° at north and then working east, south, west and back to 359°. So, in this case, the bearing to the sun, the sun’s azimuth (Zn), is the same as Z. We’ll talk more about all of these anglesand sides when we get further into how to calculate a sight reduction. This discussion was designed to familiarize you with the navigational triangle and its parts. Having a sense of triangle will help you understand celestial nav.