Editor’s note: In this installment of our celestial navigation series, we take a look at the arcane but still intriguing subject of lunar distance sights for finding time and longitude.
In this series, we’ve started from the most basic concepts and worked our way through every type of sight in celestial navigation: sun sights, star sights, planet sights, moon sights, latitude from noon, latitude from Polaris, multiple body sights and a day at sea for the celestial navigator. If you’ve followed the installments in this series, you are well set up to navigate with celestial navigation. The only thing left is to get your sextant, watch, almanac and sight reduction tables and practice the different types of sights, the reductions and the plotting. Then go on a voyage or two and use your newfound knowledge.
We’ve come so far in this series that we’ve reached the final installment. We’ve covered the basics, the solid middle ground and even advanced ideas like the immersive celestial day at sea. We’ll end the series with a discussion of a more esoteric technique that most celestial navigators will likely never use but which is a great capstone to your knowledge, if only for its historical significance to the art of navigation. The technique involves using sextant sights to determine GMT (Greenwich Mean Time). This is done by measuring something called a lunar distance.
This technique isn’t the most practical piece of knowledge for the celestial navigator in the age of GPS. It does, however, offer great insight into the lore and tradition of celestial navigation, especially for a faithful reader of this series who has already learned all the practical elements of this type of navigation and is eager to try something out of the ordinary.
The lunar
The lunar distance sight, sometimes simply called a lunar, harkens back to the beginnings of celestial navigation. Early navigators navigated using non-quantitative “eyeball” observations. They employed simple tools like the latitude hook or the Arabic kamal that gave them their latitude without having to resort to any numbers. As the science of navigation progressed, navigators began using devices with number scales, like cross-staffs and backstaffs, that required mathematical concepts to make use of those observed numbers. And while latitude could be determined accurately, the holy grail of celestial navigation continued to be the search for a way to find longitude at sea.
This search for a way to “find the longitude” became a great international race in the 17th and 18th centuries. It was the space race of its day. The British, being the premier naval power of the era, put considerable money and effort into the search. by order of Parliament a Board of Longitude was established, and it offered a substantial monetary prize to the scientist or inventor who could crack this nut.
Some of the methods proposed during this search were ingenious, while others were crackpot fantasies driven mainly by the desire to secure the £20,000 prize (the equivalent of more than $3 million today). One of the best examples of the latter was the scheme put forward by two Britons, William Whiston and Humphry Ditton. This pair devised a scheme that required ships to be anchored at set intervals across the ocean. On a regular schedule, these ships would fire incendiary shells into the air that would explode with a bright flash. Nearby navigators would note the difference between flash and bang and calculate their distance from the nearest anchored ship. Or something like that. Needless to say, this solution to the longitude problem was not put into practice and Whiston and Ditton got no prize money from the Board of Longitude.
Jupiter’s moons
Another proposal was to make use of the four largest moons of Jupiter as a kind of celestial clock. The moons’ position vis-à-vis Jupiter can be used to determine GMT and thus longitude. The technique was used successfully for surveying and other land-based applications. Observing the geometry of these tiny dots of light from the pitching deck of a ship, however, proved all but impossible. One inventor named Christopher Irwin tried to help by inventing a gimbaled “marine chair.” British Astronomer Royal Nevil Maskelyne tried the chair aboard ship in 1761 and wrote somewhat unenthusiastically, “Mr. Irwin’s marine chair affords no convenience or advantage to an observer in using a telescope for observing the celestial phenomena at sea, but rather the contrary.”
The most promising solution to the longitude problem proved to be the eventual winner: a precise marine chronometer that enabled mariners to bring GMT along with them. Though clockmaker John Harrison developed several effective chronometer models and ultimately secured the monetary prize (paid in installments between roughly 1765 and 1773), chronometers remained expensive instruments and only become standard equipment aboard ships in the mid to late 19th century.
So that leaves us with the other observational method for finding GMT, and thus longitude: the lunar. The aforementioned Astronomer Royal Maskelyne was an ardent supporter of the lunar distance technique and worked out lunar distance tables that first appeared in the British nautical almanac in 1765. This technique is still usable today and could be employed should a navigator find him or herself in the (admittedly unlikely) situation of having no working timepieces aboard.
The moon as a clock hand
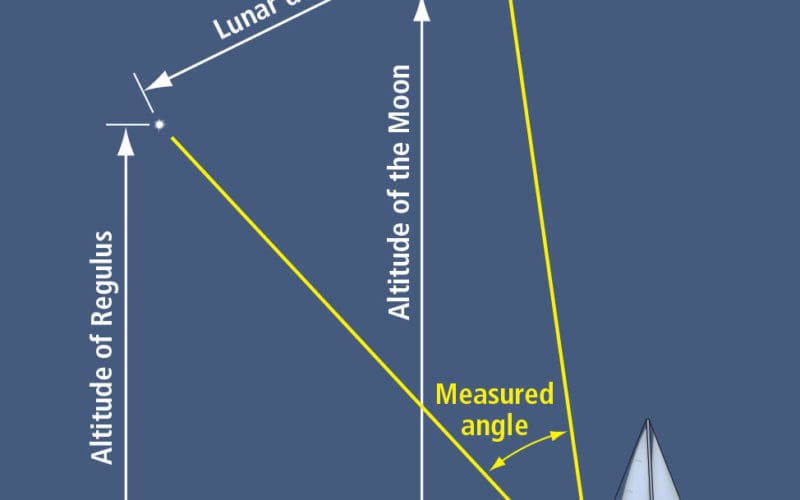
The distance in a lunar distance is actually an angle. We use our sextant to measure the angle between the moon and another celestial body, most often the sun but also a star close to the plane of the ecliptic. What we’re measuring is one part of a Great Circle between the moon and the celestial body. This measurement tells us the angular distance from the moon to that body along that Great Circle. Then we can convert the distance into the time in GMT. Let’s look at how this works by using the stars as an example. The stars are fixed in relation to each other. From our point of view on earth, the stars don’t appear to change this fixed relationship. We covered this concept previously when we explored star sights and talked about stars and their fixed sidereal hour angles (SHA). These fixed SHAs allow the Nautical Almanac to be far more condensed than if we had to list the GHA (Greenwich Hour Angle) and declination for every navigational star for every hour of every day.
The moon orbits around the earth, and as it does so it moves across this field of fixed stars at a steady rate. It goes 360 degrees around the earth in 27.3 days, or 13.2 degrees a day. This means the moon covers roughly 30 minutes of arc, or half a degree, every hour. It’s like the hand of a clock in the sky. And that’s the way we can use it with lunar distance sights to find time.
The method has several steps. The first is to measure the altitude of the moon and the other body, let’s say a star, above the horizon, the same way we do when we’re taking a sight to find a LOP (line of position). We have to correct those sights for index error (if we have any), dip and altitude correction.
Clearing the lunar distance
Next, we use our sextant to bring the limb of the moon so that it just touches the star. This is the lunar distance angle. We need to correct this sight for IE and for parallax, refraction and semidiameter, a dip correction is not necessary since we aren’t using the horizon. Correcting this sight is quaintly called “clearing the lunar distance.”
How do we convert this cleared lunar distance into a GMT time? In the past, navigators had to do work through equations using spherical trigonometry to come up with the desired time. Then, nautical almanacs included lunar distance tables that gave values for every three hours throughout the day for selected objects to use with the moon. When chronometers became widely available and the technique of lunar distance fell by the wayside, these tables ceased to be included.
What if you are a modern-day celestial navigator? Once you get your lunar distance, how do you convert that into GMT? There are books available that lay out the exact steps. A good one is John Karl’s Celestial Navigation in the GPS Age, which has a chapter on lunars that includes a flow chart and a form that lays out the spherical trig required.
Another option is to make use of Frank Reed’s comprehensive celestial navigation website, ReedNavigation.com. Reed has a section of the site devoted to lunars (reednavigation.com/lunars/) that includes web-based apps that predict lunar distances based on your DR and date and time, and an app that will calculate longitude and time from the lunar distance data you enter. Reed also has a page that goes step by step through the process of working out a lunar using spherical trig (reednavigation.com/lunars/easylun.html).
Lunars may be a specialized tool, but like all of celestial navigation, they are a satisfying skill to pick up for the complete celestial navigator who wants to know it all. n